
Другие статьи из рубрики «Дифференцированный платеж»
- Задача №1 (общая сумма выплат)
- Задача №10 (общий размер всех выплат)
- Задача №2 (минимальный срок кредитования)
- Задача №3 (определение срока кредитования)
- Задача №4 (определение срока кредитования)
- Задача №5 (нахождение процентной ставки банка)
- Задача №6 (поиск процентной ставки банка)
- Задача №7 (переплата по кредиту в %-ном отношении)
- Задача №8 (поиск процентной ставки банка)
- Задача №9 (общий размер всех выплат)
|
Содержание: |
Возникают проблемы с задачами из ЕГЭ по математике на дифференцированные платежи по кредиту?
Всем привет! Вы находитесь на моем персональном сайте подготовки к ОГЭ/ЕГЭ по математике. Также сферой моих профессиональных интересов является подготовка школьников к ОГЭ/ЕГЭ по информатике, а студентов к зачетам и экзаменам по различным языкам программирования.
Для своих потенциальных клиентов я разработал специальный финансовый фильтр, позволяющий выбрать тот формат уроков, который соответствует вашим ожиданиям. Обращаю ваше внимание на тот факт, что в настоящий момент времени, когда господствует научно-технический прогресс, большинство моих учеников занимаются дистанционно, используя, например, программу "Скайп".
Испытываете сложности в решении задач из официального экзамена ЕГЭ по математике, ориентированных на дифференцированные платежи по кредиту? Тогда срочно берите в руки телефон, набирайте мой контактный номер телефона и записывайтесь на первый пробный урок.
Условие задачи
В июле планируется взять кредит в банке на сумму $6$ миллионов рублей на срок $15$ лет.
Условия его возврата таковы:
Каждый январь долг возрастает на $q\%$ по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найти q, если известно, что наибольший годовой платеж по кредиту составит не более $1.9$ миллиона рублей, а наименьший не менее $0.5$ миллиона рублей.
Решение задачи
Вообще, когда нужно отыскать процентную ставку банка, у старшеклассников возникает множество проблем. Поэтому давайте осторожно начнем разбираться и проводить анализ постановки задачи.
Во-первых, нужно понять, о какой кредитной программе идет речь. Напомню, что можно выделить $2$ следущих программы: дифференцированные платежи по кредиту и аннуитетные выплаты по кредиту.
Но при внимательном прочтении условия задачи можно заметить намеки на то, что нужно использовать схему дифференцируемых платежей. Вот эта фраза является маркером, указывающим на это: "В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года". Это одно из базовых свойств модели дифференцируемых выплат, когда размер кредита уменьшается равными частями. Идем дальше!
Во-вторых, в обязательном порядке, нужно понимать принцип работы схемы дифференцированных платежей по кредиту, а особенно основательно разбираться в соответствующей математической модели. Эта модель - ключ к успешному решению практически всех заданий, ориентированных на дифференцированные выплаты. Обязательно познакомьтесь с этой моделью, если даже помните ее частично.
Давайте введем следующие обозначения:
| \(S\) - размер первоначального кредита | \(r\) - процентная ставка банка, выраженная в долях | \(R = 1 + r\) - для удобства расчетов |
| \(n\) - общее количество отчетных периодов | \(i\) - номер текущего отчетного периода | \(\%_{i}\) - размер начисленных банком процентов за конкретный период |
| \(p_{i}\) - размер платежа за конкретный период | \(P\) - общая сумма всех выплат/платежей | \(q\) - ставка банка, выраженная в процентах |
Подобные обозначения я использую в каждом примере, чтобы читатель не путался в переменных, когда переключается между решениями и соответствующими математическими выкладками.
Из условия вытекает, что:
| $S = 6$, млн. рублей | $n = 15$ | $p_{max} \le 1.9$ | $p_{min} \ge 0.5$ |
Наша цель отыскать значение переменной $q$. Внимательно, ищем именно $q$, а не $r$. Все-таки между ними есть небольшое отличие.
Те, кто хорошо понимает модель дифференцированных платежей по кредиту, сразу скажут, что можно точно указать, какой по счету платеж является максимальным, а, какой минимальным. Давно доказано, в том числе и мною, что в модели дифференцируемых платежей $1$-й платеж является наибольшим, а последний - наименьшим. Как все просто, да? ![]()
Значит, наши ограничения принимают вид:
$\begin{cases}p_{1} \le 1.9 \\ p_{15} \ge 0.5\end{cases}$
Осталось разобраться с тем, как математически выразить $1$-ю и $15$-ю выплаты. Нужно знать из каких составляющих состоит платеж как таковой:
| <Размер i-го платежа> = <Сумма начисленных процентов> + <Одна часть первоначального кредита> |
Одну часть первоначального кредита получаем по формуле $\frac{S}{n}$, а размер начисленных процентов за $i$-й период можно получить из этой формулы $\%_{i} = \frac{n - i + 1}{n} * S * r$. Значит:
$p_{1} = \frac{15 - 1 + 1}{15} * 6 * r + \frac{6}{15} = \frac{15}{15} * 6 * r + \frac{2}{5} = 6 * r + \frac{2}{5}$.
$p_{15} = \frac{15 - 15 + 1}{15} * 6 * r + \frac{6}{15} = \frac{1}{15} * 6 * r + \frac{2}{5} = \frac{2}{5} * r + \frac{2}{5} = \frac{2}{5} * (r + 1)$.
В итоге получаем систему, которую нужно довести до финализации:
$\begin{cases}6 * r + \frac{2}{5}\le 1.9 \\ \frac{2}{5} * (r + 1) \ge 0.5\end{cases}\:\:\leftrightarrow\:\:\begin{cases}30 * r + 2\le 9.5 \\ 2*r + 2\ge 2.5\end{cases}\:\: \leftrightarrow \:\: \begin{cases}30 * r \le 7.5 \\ 2 * r \ge 0.5 \end{cases}$
И, в итоге, образуется очень интересный вариант неравенств:
$\begin{cases}r \le 0.25 \\ r \ge 0.25 \end{cases} \:\:\:\: \leftrightarrow \:\:\: r = 0.25$
Несмотря на то, что мы решали систему неравенств, получился однозначный результат. Так как именно лишь число $0.25$ одновременно попадает в области решений обеих неравенств. Круто! ![]() Все очень просто, если фундаментально понимать модель дифференцированных платежей по кредиту.
Все очень просто, если фундаментально понимать модель дифференцированных платежей по кредиту.
Но нам нужен ответ, выраженный в процентах, а не в долях! Напомню базовую формулу, связывающую эти величины: $r = \frac{q}{100 \%}$. Очевидно, что из нее элементарно высчитывается $q$: $q = r * 100 \% = 0.25 * 100 \% = 25 \%$. А вот это уже официальный ответ к поставленной задаче!
Но как убедиться в правильности полученного ответа? А вдруг допущена ошибка! На своих индивидуальных уроках я строю верифицирующую таблицу в великолепной программе "MS Excel". В данном случае она будет иметь следующий вид:
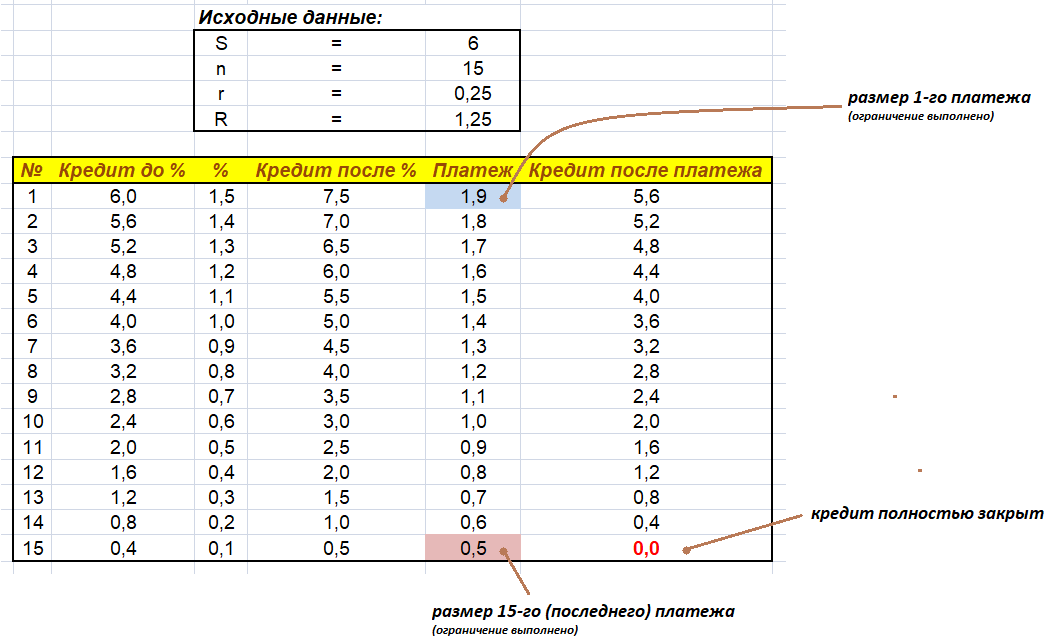
Это прекрасная аналитическая таблица, демонстрирующая все этапы дифференцированных выплат по кредиту. Внимательный $11$-классник сразу увидит множество закономерностей в колонках этой таблицы. Особенно хорошо заметны ряды значений, образующих арифметическую прогрессию.
Ответ: $25 \%$.
Выводы и рекомендации
Все упирается в хорошее понимание модели дифференцированных платежей. Кто знает эту модель - тот крайне силен в подобных задачах. Кто не знает - нужно срочно ее изучать!
В обязательном порядке нужно знать свойства дифференцируемых платежей, а также зависимости данных, которые подчиняются арифметической прогрессии.
Ну, и, разумеется, нужно правильно определять кредитную программу. Для этого я рекомендую многократно перечитывать постановку задачи, выявлять необходимые маркеры, указывающие на тип кредитных платежей.
Примеры условий реальных задач, встречающихся на ЕГЭ по математике
А сейчас я предлагаю вам самостоятельно прорешать ниже приведенные задачи на дифференцированные платежи по кредиту. Ко всем из них прилагается полноценное текстовое решение. Но, все-таки, попробуйте решить их сами, а затем сверить ответы. Конечно, если вы чувствуете, что пока не готовы решать подобные задания, то смело переходите по соответствующей ссылке и изучайте решение.
А вообще, одна из моих ролей, как профессионального репетитора по математике и информатике, контролировать ваше решение, ход ваших мыслей и предположений и давать необходимые подсказки. Поэтому, если нужна моя квалифицированная помощь, то записывайтесь ко мне на частную подготовку.
|
Пример №1 В мае планируется взять кредит в банке на сумму \(10\) миллионов рублей на \(5\) лет.
Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита? |
|
Пример №2 В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на некоторый срок.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил \(1.8\) миллиона рублей? |
|
Пример №3 В июле планируется взять кредит в банке на сумму \(20\) миллионов рублей на некоторый срок (целое число лет).
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(47\) миллионов рублей? |
|
Пример №4 В июле планируется взять кредит в банке на сумму \(16\) миллионов рублей на некоторый срок (целое число лет).
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(38\) миллионов рублей? |
|
Пример №5 В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на срок \(15\) лет.
Найти \(q\), если известно, что наибольший годовой платеж по кредиту составит не более \(1.9\) миллиона рублей, а наименьший не менее \(0.5\) миллиона рублей. |
|
Пример №6 \(15\) января планируется взять кредит в банке на покупку нового автомобиля на \(39\) месяцев.
Известно, что общая сумма выплат после полного погашения кредита на \(20\%\) больше суммы, взятой в кредит. Найдите \(q\). |
|
Пример №7 Анатолий взял банковский кредит сроком на \(9\) лет. В конце каждого года общая сумма оставшегося долга увеличивается на \(17\%\), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)? |
|
Пример №8 Анна взяла кредит в банке на срок \(12\) месяцев (\(1\) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется \(q\%\) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется "схемой с дифференцированными платежами"). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на \(13\%\) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть \(q\). |
|
Пример №9 В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей? |
|
Пример №10 \(15\) января планируется взять кредит в банке на \(15\) месяцев.
Известно, что восьмая выплата составила \(108\,000\) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования? |
Рекомендую отслеживать данный список, так как я постоянно наполняю его новыми материалами, в том числе нестандартными задачами на дифференцированные платежи по кредиту. И помните о том, что только практика и правильно подобранная программа индивидуальной подготовки, сделает вас неимоверно сильным в данной области.
Хотите научиться профессионально решать задачи на дифференцированные платежи по кредиту? Записывайтесь на частные занятия!
Я прекрасно понимаю, что на самом деле, недостаточно внимательно прочитать данную статью. Подход должен быть более глобальным и всеобъемлющим. Данное решение - лишь песчинка среди пустыни под названием "Экономические задачи".
Я - репетитор-практик! Это означает, что на своих уроках колоссальное количество времени я уделяю реальным задачам и решениям. Изучать теорию можно по классическим учебникам или посредством глобальной сети Интернет. Виртуальная среда предлагает множество сайтов, ориентированных на теоретические изыски. Правда информация очень часто является искаженной, недостоверной и неполной.
Я же для своих подопечных составляю индивидуальный план подготовки, подбираю задания, уровень сложности которых соответствует уровню "прокаченности" знаний ученика. Поэтому, если хотите заниматься решениями задач на дифференцированные платежи по кредиту, то выбирайте подходящее вам расписание и записывайтесь на $1$-й пробный урок.
И не забывайте о том, что я достаточно известный репетитор ![]() , мне перманентно поступают заявки на индивидуальное обучение, а количество ученических мест строго ограничено. Поэтому, не откладывайте собственное решение в долгий ящик и действуйте прямо сейчас. Телефон прописан в шапке данного сайта, а электронный адрес можно отыскать в подвале сайта, пройдя по ссылке "Контакты".
, мне перманентно поступают заявки на индивидуальное обучение, а количество ученических мест строго ограничено. Поэтому, не откладывайте собственное решение в долгий ящик и действуйте прямо сейчас. Телефон прописан в шапке данного сайта, а электронный адрес можно отыскать в подвале сайта, пройдя по ссылке "Контакты".
Отзывы
моих учеников

Булычев
Владимир

Самуйлов
Кирилл

Калиновский
Илья

Леонов
Никос

Ермаченков
Александр

Станислав
Блок

Ланцев
Дмитрий

Соколов
Дмитрий

Трунин
Сергей

Павленко
Илья

Ахматова
Юлия

Воробьев
Станислав

Орлов
Максим

Уфимцев
Сергей

Минаев
Сергей

Коряков
Михаил

Крылов
Антон

Камю
Константин

Белкин
Юрий

Арсеньев
Михаил

Прохоров
Дмитрий

Дмитрий
Чуков
Самые популярные статьи из других рубрик
- Каким образом я выстраиваю конечную стадию проведения индивидуальных уроков по информатике и ИКТ
- Поведение репетитора по информатике в Москве в процессе урока. Репетиторы разные, следовательно, и их поведение тоже различно!
- Каким образом я выстраиваю основную, то есть центральную стадию проведения индивидуальных уроков по информатике и ИКТ







 Закажите
Закажите Смотрите
Смотрите Напишите
Напишите Закажите
Закажите